ข้อสอบท้ายค่าย 2 ปีการศึกษา 2566 ศูนย์ สอวน. มหาวิทยาลัยเทคโนโลยีพระจอมเกล้าธนบุรี ข้อ Intersection & Sweep Line Algorithm

Author: Nagorn Phongphasura

Problem

สรุปโจทย์

จะมีการลากเส้น Zigzag ขึ้น-ลง (หรืออาจไม่ต้องสลับกันก็ได้) จำนวน $N$ ครั้ง โดย Input แต่ละตัว จะบอกว่า ในการลากเส้นครั้งนั้น จะจบที่ค่า $y$ เท่าใด (Input ตัวแรก คือ $y$ เริ่มต้น) ดังภาพ

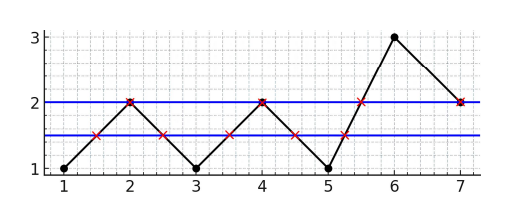
สิ่งที่ต้องทำ

หาจำนวนจุดตัดที่มากที่สุดที่เป็นไปได้ จากการลากเส้นขนานกับแกน $X$ จำนวน 1 เส้น

Constraints

$2 \leq N \leq 10^5$
$0 \leq y_1,y_2,...,y_n \leq 10^9$

Prerequisites

Sweep Line

Solution

Sweep Line Algorithm

สามารถมองโจทย์เป็นภาพง่ายๆได้ดังนี้:

ลองสมมติว่าเรามีเส้นตรงแนวนอนอยู่เส้นหนึ่ง โดยเราจะเลื่อนเส้นตรงเส้นนี้ขึ้นด้านบนเรื่อยๆ คล้ายๆเครื่องสแกน
และเราจะมีส่วนของเส้นตรงหลายๆอัน วางเรียงกันเป็นแนวตั้ง
พิจารณาว่า เมื่อเราเลื่อนเส้นตรงไปทางขวา สามารถเกิด 1 ใน 3 เหตุการณ์ดังต่อไปนี้ได้:
1. ตัดกับส่วนของเส้นตรงใหม่: ก็คือ เราจะต้องบวกจำนวนจุดตัดปัจจุบัน +1
2. พ้นออกจากส่วนของเส้นตรงเส้นใดเส้นหนึ่ง: ก็คือ เราจะต้องลบจำนวนจุดตัดปัจจุบัน -1
3. ไม่เกิดข้อ a. หรือ b. ขึ้น: ไม่ต้องทำอะไร

ซึ่งจากลักษณะแนวคิดของโจทย์ เป็นโจทย์ Classic ของ Algorithm ที่มีชื่อว่า: Sweep Line

วิธีประยุกต์สำหรับโจทย์ข้อนี้

สังเกตว่า สมมติเรามี Input $$ y_1, y_2, y_3, \dots, y_n $$ เราสามารถมองทุกคู่ของตัวเลขที่อยู่ติดกัน $(y_i, y_{i+1})$
เป็น “ช่วง” โดยในจุดเริ่มต้นของแต่ละช่วง จะมีจำนวนจุดตัดเพิ่มมา 1 และในจุดจบของแต่ละช่วง จะมีจุดตัดลดลง 1(ดังที่อธิบายไปในแนวคิดของ Sweep Line Algorithm)

ที่จุดเริ่มของช่วง ($min(y_i, y_{i+1})$) ให้เพิ่มค่า +1 หมายถึง มีช่วงหนึ่งเริ่มต้นที่นี่
ที่จุดสิ้นสุดของช่วง ($max(y_i, y_{i+1})$) ให้ลดค่า -1 หมายถึง มีช่วงหนึ่งจบลงที่นี่

เมื่อเราทำแบบนี้กับทุกช่วงแล้ว
เราจะสามารถรู้ได้ว่า ณ แต่ละ $y$ จะมีการเปลี่ยนแปลงของจำนวนจุดตัดทั้งหมดกี่จุด

จากนั้น เราแค่กวาด (Sweep) ตาม Map ที่เก็บว่ามีการเปลี่ยนแปลงของจุดตัดกี่จุด แล้วบวกค่าขึ้นเรื่อย ๆ
$$ sum \text{+= ค่าที่เปลี่ยน ณ จุดนี้} $$

ตัวแปร $sum$ จะบอกว่า “ตอนนี้มีส่วนของเส้นตรงกี่เส้นที่ยังถูกตัดอยู่” และเราก็เก็บค่า $sum$ ที่มากที่สุดที่ได้มาระหว่างการกวาด

ขั้นตอน

Input
สำหรับแต่ละคู่ของตัวเลข (ก่อนหน้า, ตัวถัดไป)
- หา $y$ เริ่มต้นของส่วนของเส้นตรงปัจจุบัน โดยการเปรียบเทียบหาค่าที่น้อยกว่าระหว่าง $y$ ปัจจุบัน กับ $y$ ก่อนหน้านี้ $(prev)$ เก็บในตัวแปรชื่อ $mn$
- หา $y$ สิ้นสุดของส่วนของเส้นตรงปัจจุบัน โดยการเปรียบเทียบหาค่าที่มากกว่าระหว่าง $y$ ปัจจุบัน กับ $y$ ก่อนหน้านี้ $(prev)$ เก็บในตัวแปรชื่อ $mx$
- เก็บใน map ว่า
  - $a[mn]$++ (เริ่มช่วง)
  - $a[mx]$-- (จบช่วง)
วนดูค่าทั้งหมดใน map ตามลำดับจากน้อยไปมาก
- เราจะ Loop ตามค่าการเปลี่ยนแปลงสำหรับแต่ละ $y$ และในแต่ละรอบที่เราวน เราจะเพิ่มค่าการเปลี่ยนแปลงไปในตัวแปร $sum$
- สร้างตัวแปร $ans$ เพื่อเก็บ $sum$ ที่มากที่สุดที่มีมา
Output

Code:

c2_kmutt_66_intersection.cpp

#include <bits/stdc++.h>
#define int long long

using namespace std;

int main() {
    cin.tie(NULL)->sync_with_stdio(false);

    // Input
    int n;
    cin >> n;

    // Map ชื่อ mp เก็บข้อมูลสำหรับแต่ละจุด
    map <int, int> mp;

    // รับ Input ตัวแรกมาก่อน เพื่อป้องกันปัญหาเรื่อง Indexing
    int prev;
    cin >> prev;

    // รับ Input ตัวอื่นๆ พร้อมกับเก็บข้อมูลใน Map
    for (int i = 1; i < n; i++) {
        int y;
        cin >> y;

        // ตั้ง mn, mx
        int mn = min(y, prev);
        int mx = max(prev, y);

        // reset prev
        prev = y;

        // เพิ่มจำนวนจุดตัด ตรง mn +1
        mp[mn]++;
        // ลดจำนวนจุดตัด ตรง mx -1
        mp[mx]--;
    }

    // กวาดเพื่อหาค่ามากสุด
    int ans = 0;
    int sum = 0;
    for (auto [idx, cnt] : mp) {
        // sum += ค่าการเปลี่ยนแปลงตรงจุดนี้
        sum += cnt;
        // ใช้ ans เก็บ sum ที่มากที่สุดที่เกิดขึ้นมาระหว่างการกวาด
        ans = max(ans, sum);
    }

    // Output
    cout << ans;

    return 0;
}

Total Time Complexity

$O(N \log N)$