คำอธิบายวิธีทำพร้อม code สำหรับโจทย์ทดสอบระบบ ข้อ toi10_goschool

Author: Nagorn Phongphasura

Problem

สรุปโจทย์

มีตาราง $M \times N$ โดยหากเราอยู่ที่ช่อง $(X, Y)$ เราจะสามารถเดินไปช่อง $(X+1, Y)$ หรือ $(X, Y+1)$ หากยังอยู่ในขอบเขต โดยจะมีหมาอยู่ในบางช่อง ที่จะทำให้เราไม่สามารถเดินไปได้

สิ่งที่ต้องทำ

หาจำนวนวิธีการเดินจากจุด $(1, 1)$ ไปยังจุด $(M, N)$ โดยที่จะไม่เจอหมา

ตัวอย่าง

พิจารณาภาพดังต่อไปนี้ $(M=5,N=4,O=3)$

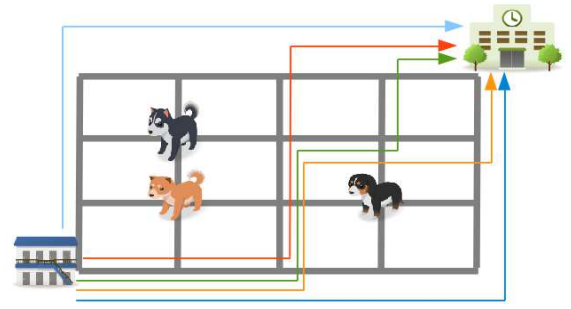
example1

จะเห็นได้ว่า จำนวนวิธีการเดินที่ไม่เจอหมาเลย เท่ากับ 5 วิธี

Constraints

$3 \leq M,N \leq 50$ (ขนาดตาราง)
$5 \leq O \leq 1500$ (จำนวนหมา)

Prerequisites

Dynamic Programming

Solution

Dynamic Programming

Dynamic Programming (DP) คือเทคนิคของการ "จำคำตอบเก่า เพื่อนำมาใช้หาคำตอบถัดไป"

ตัวอย่างที่เห็นได้ชัดคือ การหาลำดับเลข Fibonacci ซึ่งทุกคนก็รู้ดีว่า สูตรของ Fibonacci ตัวที่ $i$ $(f(i))$ จะเป็น:

\[ f(i) = \begin{cases} 1 & \text{if } i = 1 \text{ or } i = 2 \\ f(i-1) + f(i-2) & \text{otherwise} \end{cases} \]

ซึ่งหากเขียนเป็นโค้ดภาษา C++ จะสามารถเขียนได้เป็น:

fibonacci.cpp

int N;
cin >> N;
int f[N + 1];
f[1] = f[2] = 1;
for (int i = 3; i <= N; i++) {
    f[i] = f[i - 1] + f[i - 2];
}

ซึ่งถึงแม้ว่าทุกๆคนอาจจะไม่รู้ตัว แต่สิ่งนี้แหละ คือ DP เพราะครบองค์ประกอบ ได้แก่ การจำคำตอบ (เราต้องจำค่า $f$ ก่อนๆ) และ การนำคำตอบเก่ามาหาคำตอบถัดไป (ใช้สูตรเพื่อหา $f(i)$ จาก $f(i - 1), f(i-2)$)

หลักการทำ Dynamic Programming

หลักๆ จะมี 3 ขั้นตอน ได้แก่

DP Definition : กำหนดนิยาม เราจะกำหนดให้ได้ว่า $dp[i]$ จะมีความหมายเป็นอะไร ในกรณี Fibonacci จะได้ว่า $$ dp[i] = \text{the value of} f(i) $$
Base Case : ค่าเริ่มต้น ถ้าหากว่าเราต้องการที่จะหาคำตอบโดยการใช้คำตอบเก่ามาหา แน่นอนว่า เราจะต้องมี Base Case หรือ คำตอบสำหรับกรณีเริ่มต้น เพื่อที่จะนำไปต่อยอดสู่คำตอบถัดๆไปได้ ในกรณี Fibonacci จะได้ว่า Base Case คือ: $$ dp[1] = dp[2] = 1 $$ นั่นคือ $f(1) = f(2) = 1$ นั่นเอง (เพื่อจะได้นำไปใช้ในการหา $f(3), f(4), ..., f(i)$)
State Transition : คำนวณการเปลี่ยนแปลงค่า DP เนื่องจากในการเขียนโปรแกรม เราจะไม่สามารถไปนั่งแก้ไขค่าทีละตัวได้ เราจึงจะต้องกำหนด สูตรที่ตายตัวสำหรับ $dp[i]$ สำหรับการหาค่าของ $dp[i]$ ในกรณี Fibonacci จะได้สูตรดังกล่าวเป็น

\[ dp[i] = \begin{cases} 1 & \text{if } i = 1 \text{ or } i = 2 (Base Case)\\ dp[i - 1] + dp[i - 2] & \text{otherwise} \end{cases} \]

สามารถ

ดูคลิปวีดิโอ เพื่อทำความเข้าใจ DP เพิ่มเติมได้ ที่นี่
อ่านบทความ เพื่อทำความเข้าใจ DP เพิ่มเติมได้ ที่นี่ หรือ ที่นี่

วิธีทำ

สำหรับข้อนี้ เราจะนำไอเดียของ Dynamic Programming มาใช้ แต่แทนที่จะเป็น $dp$ 1 มิติ เราจะทำเป็น $dp$ 2 มิติแทน ซึ่ง DP Definition, Base Case และ State Transition จะเป็น:

DP Definition : กำหนดนิยาม $$ dp[i][j] = \text{จำนวนวิธีการเดินจาก } (1, 1) \text{ ไปยัง } (i, j) $$
Base Case : ค่าเริ่มต้น โจทย์ข้อนี้ จะมี Base Case เป็น

\[ dp[1][1] = 1 \]
State Transition : คำนวณการเปลี่ยนแปลงค่า DP

\[ dp[i][j] = \begin{cases} 0 & \text{if there is a dog at } (i,j) \\ 1 & \text{if } i = 1 \text{ and } j = 1 (Base Case) \\ dp[i-1][j] + dp[i][j-1] & \text{otherwise} \\ \end{cases} \]

เงื่อนไขแรก มาจากที่ว่า:
- เนื่องจากมีหมาอยู่ แต่โจทย์กำหนดไม่ให้พบกับหมา จำนวนวิธีที่จะไปอยู่ช่องเดียวกับหมา จึงเป็น $0$
เงื่อนไขที่สอง มาจากที่ว่า:
- กรณีอยู่ที่จุดเริ่มต้น จะมีวิธีการเดินไป ทั้งหมด 1 วิธี (Base Case)
เงื่อนไขที่สาม มาจากที่ว่า:
- สามารถเดินมาจากแถวที่ $i - 1$ ในคอลัมน์เดียวกันด้านบนได้ จึงบวกเข้าไป
- สามารถเดินมาจากคอลัมน์ที่ $j - 1$ ในแถวเดียวกันด้านซ้ายได้ จึงบวกเข้าไป

เมื่อเราไล่เก็บ DP ครบหมดแล้ว ก็สามารถตอบ $dp[m][n]$ ออกมาได้เลย (นั่นคือ พิมพ์จำนวนวิธีที่จะเดินมาช่อง $(m, n)$ ออกมา)

Code

TOI10_GoSchool.cpp

#include <bits/stdc++.h>
#define int long long

using namespace std;

int32_t main(){
    cin.tie(NULL)->sync_with_stdio(false);
    int m, n; cin >> m >> n;
    int o; cin >> o;
    int dog[m + 1][n + 1], dp[m + 1][n + 1];
    memset(dog, 0, sizeof dog);
    memset(dp, 0, sizeof dp);
    dp[1][1] = 1; // Base Case : dp[1][1] = 1
    for (int i = 0; i < o; i++) {
        int x, y;
        cin >> x >> y;
        dog[x][y] = 1;
    }
    for (int i = 1; i <= m; i++) {
        for (int j = 1; j <= n; j++) {
            // State Transition
            if (!dog[i][j]) { // ไม่มีหมา: dp[i][j] = dp[i - 1][j] + dp[i][j - 1]
                if (i > 1) dp[i][j] += dp[i - 1][j];
                if (j > 1) dp[i][j] += dp[i][j - 1];
            }
            else continue; // มีหมา: dp[i][j] = 0
        }
    }
    cout << dp[m][n];
}

Total Time Complexity

$O(MN)$