คำอธิบายวิธีทำพร้อม code สำหรับข้อ toi13_traveler

Author: Nagorn Phongphasura

Problem

สรุปโจทย์

ในอาณาจักรหนึ่งมีเมือง \(N\) เขตการปกครอง (ต่อจากนี้จะเรียกว่า เมือง) \((0\) ถึง \(N-1)\) ซึ่งระหว่างแต่ละเมือง จะมีเส้นทางรถไฟฟ้าความเร็วสูง โดย สามารถเดินทางโดยใช้รถไฟได้ทั้งสองทาง

นักวิจัยคนหนึ่ง ต้องการเดินทางจากเมือง \(X\) ไปยัง \(Y\) แต่เนื่องจากเขามีงบจำกัด จึงเดินทางได้ไม่เกิน \(Z\) กิโลเมตร โดยเขาจะเดินทางไปให้ใกล้กับเมือง \(Y\) ให้ได้มากที่สุด (ก็คือ จะไปถึงเลย ไม่ก็หาเมืองที่ใกล้ที่สุด) แล้วให้เมือง \(Y\) มารับเขาต่อ โดยหากมีเมืองที่ระยะทางจากเมือง \(Y\) ไปยังเมืองดังกล่าวเท่ากัน ให้ตอบเป็นเมืองที่มีเลขกำกับเมืองน้อยที่สุด

ตัวอย่าง

พิจารณาภาพดังต่อไปนี้ \((X = 0, Y = 5, Z = 40)\)

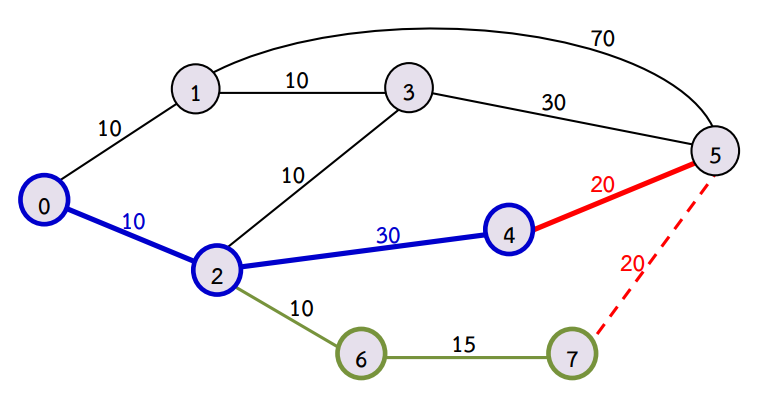
example1

จะเห็นได้ว่า นักวิจัยไม่สามารถเดินทางไปถึงเมือง \(5\) ได้ จึงต้องเลือกเมืองที่ใกล้ที่สุด นั่นคือ เมืองที่ \(4\) (เหตุผลที่ไม่เลือกเมืองที่ \(7\) เพราะว่า เลข 4 มีเลขกำกับเมืองน้อยที่สุด)

สิ่งที่ต้องทำ

หาระยะทางที่นักวิจัยจะเดินทางไปเมือง \(Y\) โดยใช้งบน้อยที่สุด หากเดินทางไปไม่ได้ จงหาระยะทางจากเมือง \(X\) ไปยังเมืองที่ทำให้ระยะทางต่อไปเมือง \(Y\) มีค่าน้อยที่สุด

Constraints

\(2 \leq N \leq 10^4\) (จำนวนเมือง)
\(1 \leq M \leq 10^5\)(จำนวนเส้นทางรถไฟฟ้าความเร็วสูง)
\(0 \leq X, Y < N, X \neq Y\) (เมืองเริ่มต้นและเมืองสิ้นสุด)
\(1 \leq Z \leq 10^9\) (งบประมาณที่มี)
\(0 \leq u_i, v_i < N\) (กำหนดเมืองที่เชื่อมของรถไฟฟ้าเส้นทางที่ \(i\))
\(1 \leq d_i \leq 10^4\) (ระยะทางของรถไฟฟ้าความเร็วสูงเส้นทางที่ \(i\))

Prerequisites

STL Basics
Shortest Paths

Solution

Idea

ถ้าหากว่าเราสามารถหาระยะสั้นสุดจากเมือง \(X\) ไปเมืองอื่นๆทุกเมือง และจากเมือง \(Y\) ไปเมืองอื่นๆทุกเมือง เราก็จะต้องทำต่อแค่ 2 ขั้นตอน ดังนี้

เช็กว่า ระยะสั้นสุดจากเมือง \(X\) ไป \(Y\) \(\leq Z\) หรือไม่ หากใช่ ก็ตอบระยะทางดังกล่าวได้เลย
หากไม่ใช่ ก็ให้ loop ตั้งแต่เมือง \(0\) ถึง \(N - 1\) แล้วทำขั้นตอนดังต่อไปนี้ (กำหนดให้เมืองที่กำลัง loop อยู่ เป็นเมืองที่ \(i\))
- ตรวจสอบว่า ระยะทางจากเมือง \(X\) ไปเมือง \(i\) \(\leq Z\) หรือไม่
  - ไม่ใช่: ข้ามไปได้เลย เพราะไม่ว่ายังไงก็ไม่สามารถเดินทางมาได้อยู่แล้ว
  - ใช่: ให้ตรวจสอบว่า ระยะทางจากเมือง \(Y\) มายังเมือง \(i\) มีค่าน้อยว่าระยะที่น้อยที่สุดที่เก็บเอาไว้หรือไม่ ถ้าใช่ ให้เก็บระยะต่ำสุดใหม่เป็นระยะจาก \(Y\) มายังเมือง \(i\) (นั่นคือ เลือกใช้เมือง \(i\) เป็นเมืองที่จะเดินทางจาก \(X\) มา แล้วให้เมือง \(Y\) มารับ)

Dijkstra's Algorithm

(อ่านว่า "ไดยก์-สตร้า's-อัล-กอ-ริ-ทึม")

เป็นอัลกอริทึมที่ใช้สำหรับการหาระยะทางที่สั้นที่สุดจาก \(1\) node (จุดยอด/เมือง) ไปยัง node อื่นๆทุก node เมื่อ edge (เส้นเชื่อมระหว่าง node) ไม่มีค่าใดเป็นลบ Time Complexity ของ Dijkstra's Algorithm คือ \(O((N + M)\) \(log\) \(N)\) เมื่อ \(N\) คือจำนวน node และ \(M\) คือจำนวน edge

หลักการทำงานของ Dijkstra's Algorithm จะอาศัยความ Greedy (เลือกวิธีที่ดีที่สุด ณ การเดิน เมื่ออยู่ที่เมืองใดเมืองหนึ่ง) มาประยุกต์ โดยขั้นตอนการทำงานจะเป็นดังนี้

สร้างตัวแปรเก็บค่าที่จำเป็น: ได้แก่
- priority_queue (min heap) เก็บ pair <int, int> \(pq\) เป็น Data Structure ที่สามารถเก็บค่าเข้าไป และดึงค่าที่ต่ำ/สูงที่สุดออกมาได้ ซึ่งใช้เวลาเพียง \(O(log\) \(N)\) (นั่นคือ เราสามารถใส่ของเข้าไปเยอะๆ เป็นชนิดใดก็ได้ \((int, string, char, pair)\) โดยตัว priority_queue จะทำการจัดเรียงให้ แล้วเมื่อเรียก pq.top() ตัว priority_queue จะคืนค่ามาเป็นค่าน้อยสุด/ค่าสูงสุดที่เราเก็บเข้าไป ตามที่เราตั้งไว้ ในที่นี้ เราจะทำให้ \(pq\) คืนค่าต่ำสุดมา) (อ่านเพิ่มเติมได้ที่นี่) โดยข้อมูลแต่ละตัวใน \(pq\) จะเก็บเป็น \(pair\) โดยจะเก็บค่าเป็น {ระยะถึงเมืองที่เก็บ, เมืองดังกล่าว} ซึ่งจากสมบัติของ priority_queue ที่จะเรียงค่าให้จากน้อยไปมาก จะทำให้ค่าที่ดึงออกมาเป็นระยะที่สั้นที่สุดเสมอ
- array \(dis\) ทำหน้าที่คอยเก็บระยะที่สั้นที่สุดจาก node เริ่มต้นไปยัง node ใดๆ เริ่มต้นโดยการตั้งระยะทุกค่าเป็นค่าสูงๆ (เนื่องจากจะสมมติว่า ยังไม่สามารถเดินทางไปยัง node ใดๆ)
ตั้งค่า: ใส่ค่าใน \(pq\) เป็น {\(0, X(เมืองเริ่มต้น)\)} แล้วตั้งค่าใน \(dis[X]\) เป็น 0 (เนื่องจากระยะทางที่สั้นที่สุดจาก \(X\) ไปยัง \(X\) เท่ากับ 0)
เริ่มดำเนินการทำงาน:
1. ใช้ while loop โดยจะ loop เมื่อ priority_queue ยังมีของข้างใน (แสดงว่า การเดินทางยังไม่จบ อาจจะหาเส้นทางที่สั้นกว่าสำหรับบาง node ได้)
2. หยิบ \(pair\) ที่อยู่ด้านบนของ \(pq\) ออกมา แล้วลบออกจาก \(pq\) (กำหนดให้เป็น {\(w, u\)} แทนระยะทางและเมืองปัจจุบัน)
3. loop ตาม node เพื่อนบ้าน ของ \(u\) (นั่นคือ node ที่มี edge เชื่อมกับ \(u\)) กำหนดให้ node นั้น มีระยะเชื่อมกับ \(u\) ยาว \(ww\) และ เป็น node หมายเลข \(v\)
  1. ตรวจสอบว่า ระยะทางรวมปัจจุบัน รวมกับ ระยะจาก \(u\) ไป \(v\) สั้นกว่าระยะสั้นสุดที่หาเจอมาแล้วหรือไม่ \((w + ww < dis[v])\)
  2. ถ้าหากว่าสั้นกว่า ก็ให้ใส่เข้าไปใน \(pq\) และอัปเดตระยะทางสั้นที่สุดใน \(dis\) เลย

ตัวอย่าง Code:

Dijkstra's Algorithm

// Dijsktra's Algorithm
// 1. เตรียมตัวแปรต่างๆ
priority_queue <pair <int, int>, vector <pair <int, int>>, greater <pair <int, int>>> pq; // การประกาศ priority_queue แบบ min_heap ซึ่งจะเรียงจากน้อยไปมากแทนที่จะเป็นมากไปน้อย
vector <int> dis(n, inf);
// 2. ตั้งค่า
dis[x] = 0;
pq.emplace(0, x);
// 3. ดำเนินการทำงาน
while (!pq.empty()) {
    auto [w, u] = pq.top(); // ดึงค่าด้านบน {ระยะทางรวม, เมืองปัจจุบัน}
    pq.pop(); // แล้วลบออก
    for (auto [ww, v] : adj[u]) {
        if (w + ww >= dis[v]) continue; // ตรวจสอบว่า ระยะทางรวม + เส้นทางใหม่ สั้นกว่าระยะทางที่สั้นที่สุดที่เคยเจอหรือไม่
        // ถ้าสั้นกว่า ก็ดำเนินการใส่ระยะใหม่ใน pq และอัปเดตค่าใน dis
        pq.emplace(w + ww, v);
        dis[v] = w + ww;
    }
}

เมื่อ loop สิ้นสุดการทำงาน เราก็จะได้ \(dis\) ซึ่งจะเก็บระยะทางที่สั้นที่สุดนั่นเอง

สามารถดู Video เพื่อให้เข้าใจการทำงานของ Dijkstra's Algorithm ได้ที่นี่ (ขอขอบคุณวิดีโอจาก Youtube: Spanning Tree)

วิธีทำ

เราสามารถใช้ Dijkstra's Algorithm โดยเริ่มต้นจากเมือง \(X\) และเมือง \(Y\) เพื่อหาระยะที่สั้นที่สุดไปยังเมืองต่างๆ แล้วทำตามขั้นตอนต่างๆที่เขียนไว้ข้างบนได้เลยยยย

Code

TOI13_Traveler.cpp

#include <bits/stdc++.h>
#define int long long

using namespace std;

const int inf = 1e18;

int32_t main(){
    cin.tie(NULL)->sync_with_stdio(false);

    // input
    int n, m, x, y, z;
    cin >> n >> m >> x >> y >> z;
    vector <pair <int, int>> adj[n];
    for(int i = 0; i < m; i++){
        int a, b, c;
        cin >> a >> b >> c;
        adj[a].emplace_back(c, b);
        adj[b].emplace_back(c, a);
    }

    priority_queue <pair <int, int>, vector <pair <int, int>>, greater <pair <int, int>>> q;

    // Dijkstra's Algorithm on X
    vector <int> dis_x(n, inf);
    dis_x[x] = 0;
    q.emplace(0, x);
    while (!q.empty()) {
        auto [w, u] = q.top();
        q.pop();
        for (auto [ww, v] : adj[u]) {
            if (w + ww >= dis_x[v]) continue;
            dis_x[v] = w + ww;
            q.emplace(w + ww, v);
        }
    }

    // Dijsktra's Algorithm on Y
    vector <int> dis_y(n, inf);
    dis_y[y] = 0;
    q.emplace(0, y);
    while (!q.empty()) {
        auto [w, u] = q.top();
        q.pop();
        for (auto [ww, v] : adj[u]) {
            if (w + ww >= dis_y[v]) continue;
            dis_y[v] = w + ww;
            q.emplace(w + ww, v);
        }
    }

    if (dis_x[y] <= z) { // หากระยะจากเมือง X ไปเมือง Y มีค่าน้อยกว่าหรือเท่ากับงบประมาณ ก็ตอบออกไปได้เลย
        cout << y << ' ' << dis_x[y] << ' ' << 0; // พิมพ์เมือง Y, ระยะทางจากเมือง X ไปเมือง Y, ระยะจากเมือง Y ไปเมือง Y (ซึ่งคือ 0 นั่นเอง)
        return 0; // จบการทำงานของโปรแกรม
    }

    int node = 0, len = inf; // ตั้งระยะที่สั้นที่สุดเป็นค่ามากๆ (ในที่นี้ กำหนด inf เป็น 10^18)
    for (int i = 0; i < n; i++) {
        if (dis_x[i] <= z && dis_y[i] < len) { // ตรวจสอบว่า ระยะจากเมือง X น้อยกว่า Z หรือไม่ และตรวจสอบอีกว่าระยะจากเมือง Y มีค่าน้อยกว่าระยะที่น้อยที่สุดที่พบมาแล้วหรือไม่  
            node = i;
            len = dis_y[i];
        }
    }

    cout << node << ' ' << dis_x[node] << ' ' << dis_y[node]; // พิมพ์เลขเมืองที่จะเดินทางไปให้มารับ, ระยะจากเมือง X, ระยะจากเมือง Y
}

Total Time Complexity

\(O((N + M)\) \(log\) \(N)\)